RESULTS

We have obtained x-ray scattering data at high instrumental resolution for the (fluid, chain melted) phase of DPPC at 50C for samples exhibiting a wide variety of D-spacings, as summarized in Table I. Smaller D-spacings occurred when higher osmotic pressure was applied by increasing the concentration of PVP. The maximum number of observable small angle lamellar scattering peaks increased as D decreased. Incidentally, we have consistently found that the D-spacing of fully hydrated DPPC (with 0% PVP) varies noticeably from sample to sample. The first two samples in Table I give the maximum range that we have observed, although it may be noted that Shipley's group (Janiak et al, 1976) has observed D-spacings as low as 60.0 Å.

 
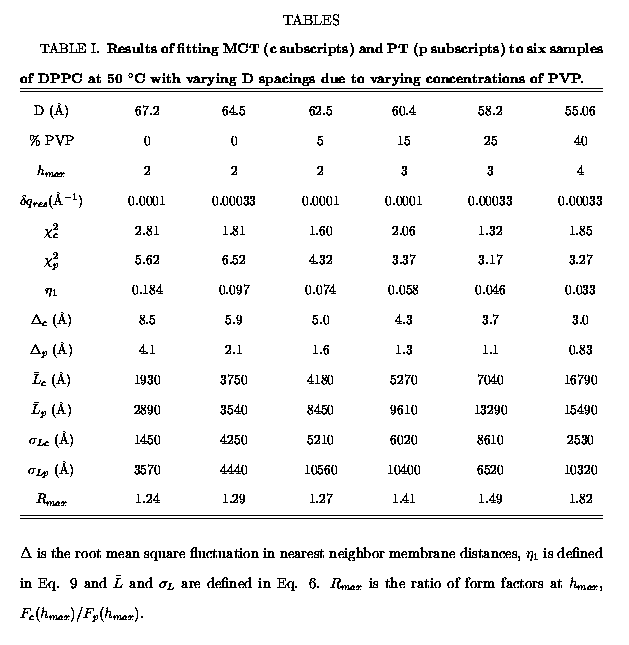
Figure 5 shows the scattering data for the DPPC sample with 0% PVP and D = 64.5 Å. Although these data were taken with the wider longitudinal resolution using the dispersive detector set-up, the peak shapes are well resolved. The PT fit to the first order peak appears visually to be nearly as good as the MCT fit, but the MCT fit to the second order peak is clearly superior. As can be seen in Table I, the ratio of the for the two theories is 3.6, indicating that MCT is far superior to PT.

Figure 6 shows the scattering for the other 0% PVP sample with D = 67.2 Å. These data were taken with our highest resolution. The scattering for Å appears to be anomalously high and erratic; these data points are not fit well by either theory and this accounts for the relatively large values of . Nevertheless, the ratio of for the two theories strongly supports the conclusion that MCT is better than PT.

Figure 7 shows scattering data for the 25% PVP sample with D = 58.2 Å. Again, although there is little difference in the fits to the first order peak, MCT clearly fits both higher order peaks better than PT. Data (not shown) for the other three samples confirms this general conclusion. We have also analysed much additional data from DPPC using only MCT with similar results that will be reported in a subsequent publication. MCT fits to less extensive data from DMPC have previously been shown by Zhang et al. (1995); these latter fits gave smaller values near 1.4 by relaxing the constraint in Eq. 10.

The best fits to the data yield the values of the parameters reported in Table I. As expected, the values of , and decrease monotonically with decreasing D as fluctuations in the multilamellar vesicles are suppressed by increased osmotic pressure. Table I shows that the root mean square fluctuations in nearest neighbor distances, which are given by for MCT (from Eq. 11) and by from the PT fit, are predicted to be larger by MCT than by PT, by a factor that varies from about 2 to nearly 4 as D decreases. The probable uncertainties in the parameters and are quite small, of order 1%. The mean domain sizes are quite large for both theories, corresponding to average number N of bilayers per domain from 30 to 300. Since the values of are comparable to the values of for both theories, the domain size distribution is quite broad.

The final row in Table I indicates how the form factors that arise from fits to the data using MCT and PT differ. Specifically, the form factors F(1) for the first order peaks are normalized to unity for the fits from both theories. The fits to the peak shapes yield S(q) shapes with amplitudes that give F(h) according to Eq. 4. Finally, for the highest order peak, , the ratio, , of the MCT form factor to the PT form factor is reported in Table I.

Finally, it may be of interest to see how our modifications to the Caille theory affect fits to the data compared to the unmodified Caille theory that was used earlier by Roux and Safinya (1988). Previous authors did not report values and it is difficult in any case to compare different experiments directly. However, we have performed fits to some of our data using the unmodified Caille theory, as shown in Fig. 8. The for the unmodified Caille theory is much larger than the for the modified theory. The unmodified theory does a good job fitting the tails; the primary reason for the larger is the difficulty in fitting the sharp first order peak and this is primarily due to the classical finite size factor which is an artificial approximation (Zhang et al., 1994). It is interesting to compare the unmodified Caille theory to PT which fits the h=1 peak better (Fig. 5) but has trouble with the h=2 peak for which the tails are larger.