A scattering theory that allows for bending of the bilayers in addition to fluctuations in the mean spacings between bilayers and that is based on energetics of both kinds of fluctuations was originally presented by Caillé (1972) who built upon the thermodynamic theory of smectic liquid crystals summarized by DeGennes (1974). This is a rather deep physical theory that gives rise to non-Bragg scattering peaks with long power law tails that conceal much of the true scattering intensity and thereby artifactually reduce the apparent form factor monotonically as a function of the order h of the peak. In the Caillé theory the primary fluctuation parameter is
which involves the bending modulus K of lipid bilayers and the bulk modulus
B for compression; the wave vector q has the value 2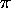
h/D at the
h-th order peak and kT is the thermal energy.
Since each peak is sharp and well separated from other peaks,
it is customary to report just 
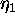, which is
defined to be the value of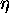 
at 
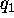for the h=1 first order peak,
recognizing that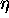 
near the h-th order peak is given by
Since the size of the peak tails relative to the central peak grows with
the size of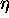 
, higher order peaks are more affected by fluctuation
artifacts than lower order peaks.
We have modified the Caillé theory in a recent theoretical
paper (Zhang et al, 1994).
Our modifications did not affect any of the qualitative results
in this theory, but they were necessary for obtaining better
quantitative fits to powder data, and particularly for extracting the correct form
factors to be used for obtaining electron density profiles. Detailed
fits to some of our data were shown in previous papers
(Zhang et al., 1995a and 1995b). The primary parameters in
these fits are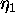 
, the mean size of domains 
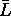and the root mean
square distribution 
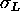of domain size as described in detail by
Zhang et al. (1994 and 1995b).
