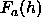 compared to the true form factors
compared to the true form factors 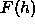 according to the approximate formula
according to the approximate formula
The modified Caillé theory (Zhang et al., 1994; Zhang, 1995) shows that
the effect of fluctuations reduces the apparent form factors 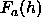 compared to the true form factors
compared to the true form factors 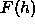 according to the approximate formula
according to the approximate formula
where C is nearly constant as a function of order h,
and 2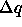 is the interval over which the data are integrated
to obtain the apparent, uncorrected intensity of the peak.
If
is the interval over which the data are integrated
to obtain the apparent, uncorrected intensity of the peak.
If 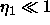 , i.e., there are several observable peaks,
the apparent electron density
, i.e., there are several observable peaks,
the apparent electron density 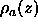 , obtained from the
apparent form factors
, obtained from the
apparent form factors 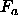 in Eq. A1, are related
to the true electron density
in Eq. A1, are related
to the true electron density 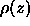 by
the following convolution integral
by
the following convolution integral
where
We call U(z) the smearing function; it is essentially a Gaussian whose half width at half maximum,
depends strongly on 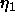 . Figure 11 shows
how a typical U(z) smearing function broadens the
electron density features of a hybrid model.
However, the apparent head to head distance
. Figure 11 shows
how a typical U(z) smearing function broadens the
electron density features of a hybrid model.
However, the apparent head to head distance 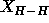 is basically unchanged from the true distance; this latter result
can be understood theoretically because the convolution of a Gaussian smearing
function with a symmetric headgroup peak leaves the center of the
resulting peak position unchanged.
is basically unchanged from the true distance; this latter result
can be understood theoretically because the convolution of a Gaussian smearing
function with a symmetric headgroup peak leaves the center of the
resulting peak position unchanged.
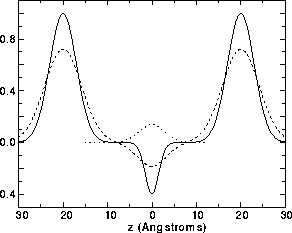
Figure 11: Smearing effect on electron density due to fluctuations.
The solid line shows an unsmeared profile that is convoluted with
the smearing function shown by the dotted line to produce the
smeared electron density profile shown by the dashed line.
The calculation of the smearing function used
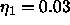 and
and 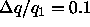 .
.
Traditionally, the smearing effect shown in Fig. 11 was treated by assuming that the true form factor was multiplied by an ad hoc Debye-Waller type of temperature factor (Franks and Lieb, 1979; Torbet and Wilkins, 1976; Zacai et al., 1975)
The 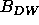 factor for a rather dry bilayer system was taken to be zero;
and
factor for a rather dry bilayer system was taken to be zero;
and 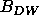 for a higher water content bilayer system was then
determined by matching the
for a higher water content bilayer system was then
determined by matching the 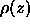 for that
high water content bilayer system with the
for that
high water content bilayer system with the
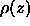 calculated using
calculated using 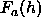 in Eq. A6 and
in Eq. A6 and 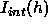 data from the very low water content bilayer system,
assuming that the bilayer structure does not change within
that hydration range.
Eq. A6 has a very similar form to Eq. A1.
However, in contrast to the use of Eq. A6, in our use of
Eq. A1 the parameter
data from the very low water content bilayer system,
assuming that the bilayer structure does not change within
that hydration range.
Eq. A6 has a very similar form to Eq. A1.
However, in contrast to the use of Eq. A6, in our use of
Eq. A1 the parameter 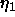 is determined by fitting
the peak shapes. Therefore, our theory does not require the assumption
that the bilayer shape is unchanged and therefore allows us to test it.
Although one could devise a similar procedure based upon Eq. A6,
this requires an additional unknown Debye-Waller parameter
is determined by fitting
the peak shapes. Therefore, our theory does not require the assumption
that the bilayer shape is unchanged and therefore allows us to test it.
Although one could devise a similar procedure based upon Eq. A6,
this requires an additional unknown Debye-Waller parameter 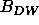 for each data set from samples with different water content.
Therefore, while our method justifies the form of the older method,
it also improves upon it.
for each data set from samples with different water content.
Therefore, while our method justifies the form of the older method,
it also improves upon it.