


Next:
Up: X-ray Structure Determination of Fully
Previous: and Other Quantities
Our primary experimental results are the ratios of form factors 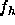 reported
in Table I for various levels of hydration. These data
provide a basic test for theoretical models of
reported
in Table I for various levels of hydration. These data
provide a basic test for theoretical models of 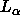 phase DPPC
bilayers, such as those
obtained from computer simulations, much like the traditional
phase DPPC
bilayers, such as those
obtained from computer simulations, much like the traditional
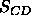 NMR order parameters (Seelig, 1977) that are most frequently employed as a test.
To perform this test electron density profiles obtained by theory should
be Fourier transformed to obtain
NMR order parameters (Seelig, 1977) that are most frequently employed as a test.
To perform this test electron density profiles obtained by theory should
be Fourier transformed to obtain 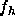 .
.
The particular innovation used in this study to obtain the 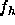 is the combined use of x-ray scattering at very high instrumental
resolution and the modified Caillé peak shape theory
(Zhang et al., 1994) to obtain the true scattering intensity under the
entire peak, including the long power law tails predicted by this theory
and verified experimentally (Roux and Safinya, 1988; Zhang et al., 1995b).
This analysis obtains
the Caillé
is the combined use of x-ray scattering at very high instrumental
resolution and the modified Caillé peak shape theory
(Zhang et al., 1994) to obtain the true scattering intensity under the
entire peak, including the long power law tails predicted by this theory
and verified experimentally (Roux and Safinya, 1988; Zhang et al., 1995b).
This analysis obtains
the Caillé 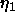 fluctuation parameter which is shown in Fig. 2
and which decreases as D-spacing decreases. From the definition of
fluctuation parameter which is shown in Fig. 2
and which decreases as D-spacing decreases. From the definition of 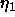 following Eq. 1, this suggests that the compression modulus
B increases with dehydration and that the interactions between bilayers
become stronger as the water space decreases.
Further analysis of the forces involved will be deferred to another paper.
Most importantly for this paper,
this analysis of the experimental data is essential to obtain
the correct continuous scattering transform F(q) and to explain why
some of the higher order peaks for the more hydrated samples can not be seen.
following Eq. 1, this suggests that the compression modulus
B increases with dehydration and that the interactions between bilayers
become stronger as the water space decreases.
Further analysis of the forces involved will be deferred to another paper.
Most importantly for this paper,
this analysis of the experimental data is essential to obtain
the correct continuous scattering transform F(q) and to explain why
some of the higher order peaks for the more hydrated samples can not be seen.
Our F(q) transform in Fig. 4 is consistent with no change in
bilayer structure for the 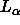 phase of DPPC as the bilayer
is dehydrated from a D-spacing of 67.2Å to 53.9Å. As is shown
by Fig. 5, this conclusion can not be drawn if one performs a
straightforward integration of the central peak intensities that ignores the
long power law tails. Even the form factors for the h=2 order are
systematically too small with higher hydration, and some of the h=3
orders should have been seen, but could not be. However, we now know that
this is due to the loss of intensity into the tails, which is impossible to separate
from background without an appropriate theory to perform the extrapolation
from the measured peak shapes. This in turn requires high resolution
x-ray detection that was achieved with our experimental configuration at CHESS.
phase of DPPC as the bilayer
is dehydrated from a D-spacing of 67.2Å to 53.9Å. As is shown
by Fig. 5, this conclusion can not be drawn if one performs a
straightforward integration of the central peak intensities that ignores the
long power law tails. Even the form factors for the h=2 order are
systematically too small with higher hydration, and some of the h=3
orders should have been seen, but could not be. However, we now know that
this is due to the loss of intensity into the tails, which is impossible to separate
from background without an appropriate theory to perform the extrapolation
from the measured peak shapes. This in turn requires high resolution
x-ray detection that was achieved with our experimental configuration at CHESS.
We conclude from our data that the threshold spacing 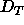 ,
above which the bilayer structure effectively does not change, must be
smaller than 54Å.
This conclusion is supported by the results of Torbet and Wilkins
(1976) for the gel phase of DPPC which showed that fairly small changes
in bilayer thickness resulted in rather large changes in the continuous
transform. This conclusion disagrees with
conclusions drawn from x-ray studies using the gravimetric method of
Luzzati which indicated that bilayer structure changed continuously
as the system is dehydrated from full hydration (Tardieu et al., 1973; Lis et al., 1982).
The latter conclusion had implied that results from studies on partially dehydrated
samples, such as the classic neutron diffraction studies on
specifically deuterated lipids (Buldt et al., 1979; Zaccai et al., 1979)
where the D-spacing was 54.1Å, are biologically less relevant.
One likely source of error in the
gravimetric method is the assumption that all the water resides neatly between
the bilayers (Wiener et al., 1989; Klose et al., 1988). This is
quite unlikely for multilamellar vesicles that must have
extra water in small volumes in the center of each MLV as well as in
regions between different MLVs. Only in well-oriented planar
arrays could one hope that this assumption is valid.
Also, the areas A from gravimetric studies have been consistently
larger than those obtained by other methods; this discrepancy is also
explained by the assumption about water residence being incorrect. In the case of gel
phase DPPC, we have shown previously for both oriented (Tristram-Nagle et al., 1993)
and powder, multilamellar vesicular samples (Sun et al., 1994),
that the gravimetric method gave erroneously large results for A.
Although our present results do not go to low enough hydration to
find the value of the dehydration threshold
,
above which the bilayer structure effectively does not change, must be
smaller than 54Å.
This conclusion is supported by the results of Torbet and Wilkins
(1976) for the gel phase of DPPC which showed that fairly small changes
in bilayer thickness resulted in rather large changes in the continuous
transform. This conclusion disagrees with
conclusions drawn from x-ray studies using the gravimetric method of
Luzzati which indicated that bilayer structure changed continuously
as the system is dehydrated from full hydration (Tardieu et al., 1973; Lis et al., 1982).
The latter conclusion had implied that results from studies on partially dehydrated
samples, such as the classic neutron diffraction studies on
specifically deuterated lipids (Buldt et al., 1979; Zaccai et al., 1979)
where the D-spacing was 54.1Å, are biologically less relevant.
One likely source of error in the
gravimetric method is the assumption that all the water resides neatly between
the bilayers (Wiener et al., 1989; Klose et al., 1988). This is
quite unlikely for multilamellar vesicles that must have
extra water in small volumes in the center of each MLV as well as in
regions between different MLVs. Only in well-oriented planar
arrays could one hope that this assumption is valid.
Also, the areas A from gravimetric studies have been consistently
larger than those obtained by other methods; this discrepancy is also
explained by the assumption about water residence being incorrect. In the case of gel
phase DPPC, we have shown previously for both oriented (Tristram-Nagle et al., 1993)
and powder, multilamellar vesicular samples (Sun et al., 1994),
that the gravimetric method gave erroneously large results for A.
Although our present results do not go to low enough hydration to
find the value of the dehydration threshold 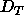 , they do require
that
, they do require
that 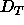 be smaller than 54Å and this suffices to validate the
biological relevance of the neutron diffraction results for
be smaller than 54Å and this suffices to validate the
biological relevance of the neutron diffraction results for 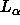 phase DPPC at
phase DPPC at 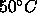 as well as
to provide support for x-ray studies that attempt to obtain membrane
structure for partially dehydrated samples.
as well as
to provide support for x-ray studies that attempt to obtain membrane
structure for partially dehydrated samples.
On the other hand, since one would expect that dehydration would alter
the forces between bilayers and that this could change their
structure, it is worth discussing quantitatively how much dehydration
was required to obtain samples with D=54Å.
In Table II it is shown that only a little less than half the
water must be removed, leaving 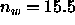 waters even when
waters even when 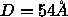 .
This is even more water than resides in the fully hydrated gel phase.
Also, the mean pure water spacing
.
This is even more water than resides in the fully hydrated gel phase.
Also, the mean pure water spacing 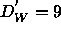 Å between headgroups is
still large enough to avoid much direct contact between headgroups
on adjacent bilayers because, as shown by Zhang et al. (1995b),
the mean fluctuation in adjacent bilayer
spacing is only about
Å between headgroups is
still large enough to avoid much direct contact between headgroups
on adjacent bilayers because, as shown by Zhang et al. (1995b),
the mean fluctuation in adjacent bilayer
spacing is only about 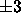 Å for the value of
Å for the value of 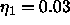 that is obtained for D = 54Å from Fig. 2.
Furthermore, the relative humidity for our most dehydrated
samples is still about 98%. In addition, we have performed differential
scanning calorimetry on
this sample and find that the main transition temperature
that is obtained for D = 54Å from Fig. 2.
Furthermore, the relative humidity for our most dehydrated
samples is still about 98%. In addition, we have performed differential
scanning calorimetry on
this sample and find that the main transition temperature 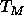 rises
at most
rises
at most 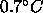 ; this is much less than the rise in
; this is much less than the rise in 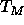 for
fully dehydrated samples which exceeds
for
fully dehydrated samples which exceeds 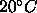 . Finally,
the work W done against the hydration force is given by the
product of the osmotic pressure of our most dehydrated
sample (
. Finally,
the work W done against the hydration force is given by the
product of the osmotic pressure of our most dehydrated
sample (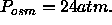 ), the area
), the area 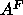 and the decay length
and the decay length
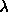 , which is given as 1.7Å for egg lecithin (McIntosh and Simon, 1986a);
this yields 0.03 kcal/mol, which is considerably less than the
enthalpy 8.7kcal/mol for the main phase transition which sets the
scale for major structural changes. Therefore, our experimental
result that bilayer structure does not change measurably upon dehydrating
to D=54Å is theoretically plausible and consistent with our
determination of structure reported in Table II.
, which is given as 1.7Å for egg lecithin (McIntosh and Simon, 1986a);
this yields 0.03 kcal/mol, which is considerably less than the
enthalpy 8.7kcal/mol for the main phase transition which sets the
scale for major structural changes. Therefore, our experimental
result that bilayer structure does not change measurably upon dehydrating
to D=54Å is theoretically plausible and consistent with our
determination of structure reported in Table II.
It may also be noted that the threshold hypothesis implies that there
is unlikely to be any structural difference between bilayers in large
unilamellar vesicles and those in multilamellar vesicles.
This follows because the inter-bilayer interactions become
considerably stronger upon dehydration. If these increasingly stronger
interactions do not change the bilayer structure, then the weaker interbilayer
forces present in fully hydrated multilamellar vesicles would not change the
bilayer structure compared to isolated large unilamellar vesicles.
Electron density profiles have been obtained in two ways. The first
and most straightforward way that has been employed by many previous
workers is to plot the Fourier series using the
maximum number of orders of diffraction, which for our data is
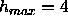 . Earlier use of this procedure has also indicated
that the thickness of bilayers does not change upon dehydrating with
PVP for either the gel phase of DPPC or the
. Earlier use of this procedure has also indicated
that the thickness of bilayers does not change upon dehydrating with
PVP for either the gel phase of DPPC or the 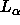 phase of
egg lecithin (McIntosh, 1986a). One of our concerns with this earlier conclusion
was that fluctuation corrections were not made
and that this would be expected to distort the form factors as shown
in Fig. 5 compared to Fig. 4. However, our result in Fig. 6 and our
theory in the Appendix shows that fluctuation corrections have almost
no effect upon the apparent head-head spacing
phase of
egg lecithin (McIntosh, 1986a). One of our concerns with this earlier conclusion
was that fluctuation corrections were not made
and that this would be expected to distort the form factors as shown
in Fig. 5 compared to Fig. 4. However, our result in Fig. 6 and our
theory in the Appendix shows that fluctuation corrections have almost
no effect upon the apparent head-head spacing 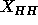 and this was
the major result required by the earlier work. Since only the
widths of the peaks and the methyl troughs are affected, our results
therefore support the methodology of the earlier work as well as the
conclusion that there is little change in bilayer structure upon mild dehydration.
and this was
the major result required by the earlier work. Since only the
widths of the peaks and the methyl troughs are affected, our results
therefore support the methodology of the earlier work as well as the
conclusion that there is little change in bilayer structure upon mild dehydration.
A major goal that we believe we have achieved is to obtain the area 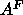 for
for 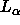 phase DPPC at 50
phase DPPC at 50 C, which is the most commonly
compared temperature. Although
C, which is the most commonly
compared temperature. Although 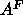 does not depend upon hydration down
to the
does not depend upon hydration down
to the 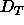 threshold, it is expected to depend fairly strongly on
temperature, especially near the main transition
threshold, it is expected to depend fairly strongly on
temperature, especially near the main transition 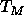 (Zhang et al., 1995a),
as well as exhibiting a gradual increase with increasing T above
50
(Zhang et al., 1995a),
as well as exhibiting a gradual increase with increasing T above
50 C, but we have not included these effects in this study.
Our primary method was adapted from one introduced by McIntosh and Simon (1986b)
that obtains
C, but we have not included these effects in this study.
Our primary method was adapted from one introduced by McIntosh and Simon (1986b)
that obtains 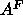 for the
for the 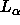 phase from Eq. 7 which uses
gel phase quantities (Tristram-Nagle et al., 1993; Sun et al., 1994),
measured volume changes (Nagle and Wiener, 1988) and the changes in
the head-head positions,
phase from Eq. 7 which uses
gel phase quantities (Tristram-Nagle et al., 1993; Sun et al., 1994),
measured volume changes (Nagle and Wiener, 1988) and the changes in
the head-head positions, 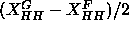 ,
which are obtained in this paper. The Fourier method
works quite well, yielding
,
which are obtained in this paper. The Fourier method
works quite well, yielding 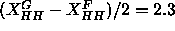 Å
and
Å
and 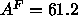 Å
Å , despite having only three samples with
, despite having only three samples with 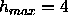 orders.
orders.
We have also used a method of analysis that treats all the data with different D-spacings
globally. This method requires a model electron density function.
We have used the hybrid model proposed earlier (Nagle and Wiener, 1989) after
showing in Fig. 7 that it adequately represents the electron density profiles
of current molecular dynamics simulations, which also agree with the main
assumption that the methylene density is effectively constant in the
hydrocarbon region as shown in Fig. 8. There are three constraints
on the electron density profile (Nagle and Wiener, 1989) that have been
employed to yield the various experimental electron density
profiles as shown in Fig. 9. Our methodology for calculating
area using Eq. 8 then yields 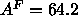 Å
Å .
.
The values of 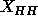 in the experimental electron density profiles in
Fig. 9 are in excellent agreement with the recent simulation of
Tu et al. (1995), also shown in Fig. 9,
which has
in the experimental electron density profiles in
Fig. 9 are in excellent agreement with the recent simulation of
Tu et al. (1995), also shown in Fig. 9,
which has 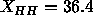 Å. One discrepancy that
arises is that use of this value of
Å. One discrepancy that
arises is that use of this value of 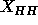 in Eq. 7 yields
in Eq. 7 yields
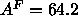 Å
Å which is larger than
which is larger than
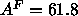 Å
Å obtained from the simulation. However, the same
spatial resolution and methodology should be used for both the gel and the
fluid phases in calculating the difference in
obtained from the simulation. However, the same
spatial resolution and methodology should be used for both the gel and the
fluid phases in calculating the difference in 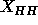 , so that we
should use the value
, so that we
should use the value 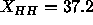 Å obtained from a 1G fit to
the simulated electron density profile (see Fig. 7). This
yields
Å obtained from a 1G fit to
the simulated electron density profile (see Fig. 7). This
yields 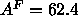 Å
Å from Eq. 7 which is satisfactorily close
to
from Eq. 7 which is satisfactorily close
to 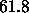 Å
Å and supports our methodology for obtaining
and supports our methodology for obtaining 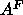 .
Another minor inconsistency arises from
applying Eq. 8 to our 1G fit to the simulated
methyl trough of Tu et al. (1995). This yields
.
Another minor inconsistency arises from
applying Eq. 8 to our 1G fit to the simulated
methyl trough of Tu et al. (1995). This yields 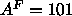 Å
Å assuming
that
assuming
that 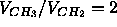 and that
and that 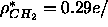 Å
Å ;
the latter value appears consistent with the simulated curve in
Fig. 9 and also emerges from our 1G fit to these data. However,
the plateau level for the number density in Fig. 8 gives
;
the latter value appears consistent with the simulated curve in
Fig. 9 and also emerges from our 1G fit to these data. However,
the plateau level for the number density in Fig. 8 gives
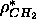 closer to
closer to 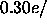 Å
Å . Using this latter value of
. Using this latter value of
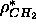 changes the size of the methyl trough so
that
changes the size of the methyl trough so
that 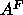 then yields 62Å
then yields 62Å using Eq. 8. While
this removes the inconsistency, it warns one that, despite the good fit of
the 1G model to the simulated data, the parameters for
using Eq. 8. While
this removes the inconsistency, it warns one that, despite the good fit of
the 1G model to the simulated data, the parameters for
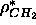 that emerge from the fit seem to be corrupted
by mixing with other parameters so that Eq. 8 does not
give accurate values for
that emerge from the fit seem to be corrupted
by mixing with other parameters so that Eq. 8 does not
give accurate values for 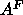 . Another discrepancy is that
our hybrid model headgroup peaks are much higher
than the simulated headgroup peaks in Fig. 9. In this latter regard,
our best hybrid model result shown by the solid line in
Fig. 9 agrees better with the simulations of
Feller et al. (1995) shown in Fig. 7, even though these simulations
were performed at a larger constant area of
. Another discrepancy is that
our hybrid model headgroup peaks are much higher
than the simulated headgroup peaks in Fig. 9. In this latter regard,
our best hybrid model result shown by the solid line in
Fig. 9 agrees better with the simulations of
Feller et al. (1995) shown in Fig. 7, even though these simulations
were performed at a larger constant area of 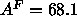 Å
Å and consequently have a smaller
and consequently have a smaller 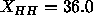 Å when fitted to
a 1G model.
Å when fitted to
a 1G model.
The most surprising result in Fig. 9 is the relative narrowness
of our headgroup peaks and the methyl trough. The 1G methyl trough
for our fully constrained fit has a half-width
(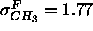 Å), not much wider than the
1G methyl trough for the gel phase (
Å), not much wider than the
1G methyl trough for the gel phase (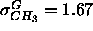 Å)
and narrower than the Gaussian fit to the simulation methyl trough
(
Å)
and narrower than the Gaussian fit to the simulation methyl trough
(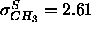 Å). The 1G headgroups have half-widths
(
Å). The 1G headgroups have half-widths
(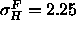 Å) which are narrower than the gel phase
results (
Å) which are narrower than the gel phase
results (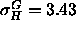 Å) and the fluid phase simulations
(
Å) and the fluid phase simulations
(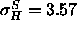 Å). It is possible that the narrowness of our
model electron density profiles is related to intrinsic errors
in analytically continuing the F(q) curve to high q. Although
the lack of data at higher angles always broadens
features in Fourier reconstructions of the electron density profile,
this is not necessarily the case for the model method,
as we have confirmed by taking a known model electron density profile,
Fourier analyzing it, adding noise to the Fouriers, fitting models
to the Fouriers, and then comparing to the original model
electron density.
Finally, when we did a fit with all three constraints, but with
Å). It is possible that the narrowness of our
model electron density profiles is related to intrinsic errors
in analytically continuing the F(q) curve to high q. Although
the lack of data at higher angles always broadens
features in Fourier reconstructions of the electron density profile,
this is not necessarily the case for the model method,
as we have confirmed by taking a known model electron density profile,
Fourier analyzing it, adding noise to the Fouriers, fitting models
to the Fouriers, and then comparing to the original model
electron density.
Finally, when we did a fit with all three constraints, but with
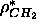 fixed to 0.304e/Å
fixed to 0.304e/Å , the methyl trough half-width
increased substantially to
, the methyl trough half-width
increased substantially to 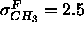 Å. In contrast,
Å. In contrast,
 only increased by 0.1Å, so widths of features in the
hybrid model may be less certain than the head-head spacing,
which is the crucial quantity for obtaining the area
only increased by 0.1Å, so widths of features in the
hybrid model may be less certain than the head-head spacing,
which is the crucial quantity for obtaining the area 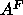 .
.
Our main result that bilayer structure does not change with
mild dehydration down to 54Å allows us to use the
older neutron diffraction
results, which were obtained for 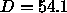 Å, in two new ways to
obtain additional estimates,
Å, in two new ways to
obtain additional estimates, 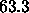 Å
Å and
and 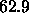 Å
Å , for
, for 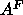 .
For our final estimate of
.
For our final estimate of 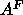 , we averaged these with
two x-ray results,
, we averaged these with
two x-ray results, 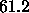 Å
Å from Fourier analysis and
from Fourier analysis and 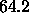 Å
Å from hybrid modeling to obtain our final diffraction result,
from hybrid modeling to obtain our final diffraction result,
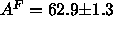 Å
Å in the
in the 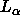 phase of DPPC at 50
phase of DPPC at 50 C.
C.
The other major way of determining 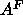 uses the
uses the 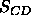 NMR order parameters.
Although the NMR method has been
employed in several different ways giving considerably different values
of
NMR order parameters.
Although the NMR method has been
employed in several different ways giving considerably different values
of 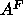 , our recent analysis gave
, our recent analysis gave 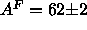 Å
Å for DPPC under the same conditions as in this paper (Nagle, 1993), in
good agreement with the present diffraction result. Even the sign of the
small difference can be understood because the NMR result assumed no
backtracking of chains, which, if present, would increase the NMR estimate
of
for DPPC under the same conditions as in this paper (Nagle, 1993), in
good agreement with the present diffraction result. Even the sign of the
small difference can be understood because the NMR result assumed no
backtracking of chains, which, if present, would increase the NMR estimate
of 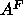 . As more quantitative information about backtracking becomes
available from simulations, quantitative changes in the NMR estimate
can be made.
. As more quantitative information about backtracking becomes
available from simulations, quantitative changes in the NMR estimate
can be made.
Our value of 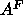 is smaller than the value
is smaller than the value 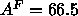 Å
Å determined for unilamellar vesicles by Lewis and Engelman (1983) using weak
continuous scattering. It is
considerably smaller than the
determined for unilamellar vesicles by Lewis and Engelman (1983) using weak
continuous scattering. It is
considerably smaller than the 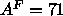 Å
Å obtained by
the gravimetric method (Lis et al., 1982) or the
obtained by
the gravimetric method (Lis et al., 1982) or the 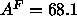 Å
Å obtained
by modifying that method (Rand and Parsegian, 1989) to try to account
for inconsistency with lateral compressibility data. This latter value of
obtained
by modifying that method (Rand and Parsegian, 1989) to try to account
for inconsistency with lateral compressibility data. This latter value of 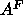 was assumed in the simulations of Feller et al. (1995). A recent simulation
(Essmann et al., 1995) used a fixed value
was assumed in the simulations of Feller et al. (1995). A recent simulation
(Essmann et al., 1995) used a fixed value 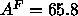 Å
Å for
nearly fully hydrated DPPC with
for
nearly fully hydrated DPPC with 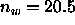 . Other recent simulations
employ constant pressure ensembles rather than constant area
ensembles and this allows for the simulation to determine the best
. Other recent simulations
employ constant pressure ensembles rather than constant area
ensembles and this allows for the simulation to determine the best 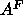 .
Chiu et al. (1995) obtain the rather smaller
.
Chiu et al. (1995) obtain the rather smaller
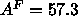 Å
Å at 52
at 52 C, but this was for DMPC. The recent simulations
for DPPC by Tu et al. (1995) yield
C, but this was for DMPC. The recent simulations
for DPPC by Tu et al. (1995) yield 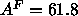 Å
Å , in excellent
agreement with our values for
, in excellent
agreement with our values for 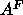 .
.
The variety of simulation results for ostensibly the same lipid bilayer
emphasizes that there are many non-canonical choices to be made when doing
a simulation. It is clearly important that critical experimental data be
available to test choices in potentials, effect of initial configuration
(since effective running times are only nsec, during which the system
may hang in a metastable state), and choice of ensemble parameters
such as effective lateral pressure. In this regard, we emphasize that
the ratios of form factors in Table I should be compared to simulations.
(Direct comparison to our primary
data, the scattering peaks, would require simulations on bilayers of
square micron size, which is rather unlikely to be feasible.) However,
we emphasize that simulation results, even if all the simulation choices
are not perfect and even if all the simulations do not agree,
are extremely valuable in testing assumptions used
in analyzing data, as we show in Figs. 7 and 8 in this paper and as was
previously mentioned in the analysis of NMR data (Nagle, 1993).
Fluid 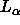 phase lipid bilayers are difficult to study experimentally,
due to their partially ordered/disordered nature which gives rise
to non-trivial fluctuations. We believe the present study has made
substantial progress on this point. We anticipate that combined experimental
and simulation studies will resolve remaining issues and provide a
methodological foundation for quantitatively comparing bilayers composed of
different lipids.
phase lipid bilayers are difficult to study experimentally,
due to their partially ordered/disordered nature which gives rise
to non-trivial fluctuations. We believe the present study has made
substantial progress on this point. We anticipate that combined experimental
and simulation studies will resolve remaining issues and provide a
methodological foundation for quantitatively comparing bilayers composed of
different lipids.
Acknowledgments: For providing the results of molecular dynamics simulations
shown in Figures 7 and 8, we thank the members of three simulation groups,
particularly Scott Feller, Richard Venable and Richard Pastor; Larry Scott;
Michael Klein, Doug Tobias and especially Kechuan Tu for visits to our
laboratory and extensive interaction.
We thank our CHESS collaborators R. L. Headrick and T. C. Irving for
their help in acquiring the basic scattering data.
Synchrotron beam time was provided under CHESS proposal P619.
This research was supported by NIH Grant No. GM44976.



Next:
Up: X-ray Structure Determination of Fully
Previous: and Other Quantities
This document was converted to HTML by Nikolai Gouliaev on Fri Oct 4 15:28:39 EDT 1996
Your comments are welcome at gouliaev@andrew.cmu.edu
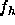 reported
in Table I for various levels of hydration. These data
provide a basic test for theoretical models of
reported
in Table I for various levels of hydration. These data
provide a basic test for theoretical models of 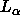 phase DPPC
bilayers, such as those
obtained from computer simulations, much like the traditional
phase DPPC
bilayers, such as those
obtained from computer simulations, much like the traditional
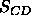 NMR order parameters (Seelig, 1977) that are most frequently employed as a test.
To perform this test electron density profiles obtained by theory should
be Fourier transformed to obtain
NMR order parameters (Seelig, 1977) that are most frequently employed as a test.
To perform this test electron density profiles obtained by theory should
be Fourier transformed to obtain 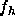 .
.
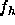 is the combined use of x-ray scattering at very high instrumental
resolution and the modified Caillé peak shape theory
(Zhang et al., 1994) to obtain the true scattering intensity under the
entire peak, including the long power law tails predicted by this theory
and verified experimentally (Roux and Safinya, 1988; Zhang et al., 1995b).
This analysis obtains
the Caillé
is the combined use of x-ray scattering at very high instrumental
resolution and the modified Caillé peak shape theory
(Zhang et al., 1994) to obtain the true scattering intensity under the
entire peak, including the long power law tails predicted by this theory
and verified experimentally (Roux and Safinya, 1988; Zhang et al., 1995b).
This analysis obtains
the Caillé 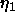 fluctuation parameter which is shown in Fig.
fluctuation parameter which is shown in Fig. 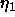 following Eq.
following Eq. 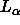 phase of DPPC as the bilayer
is dehydrated from a D-spacing of 67.2Å to 53.9Å. As is shown
by Fig.
phase of DPPC as the bilayer
is dehydrated from a D-spacing of 67.2Å to 53.9Å. As is shown
by Fig. 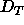 ,
above which the bilayer structure effectively does not change, must be
smaller than 54Å.
This conclusion is supported by the results of Torbet and Wilkins
(1976) for the gel phase of DPPC which showed that fairly small changes
in bilayer thickness resulted in rather large changes in the continuous
transform. This conclusion disagrees with
conclusions drawn from x-ray studies using the gravimetric method of
Luzzati which indicated that bilayer structure changed continuously
as the system is dehydrated from full hydration (Tardieu et al., 1973; Lis et al., 1982).
The latter conclusion had implied that results from studies on partially dehydrated
samples, such as the classic neutron diffraction studies on
specifically deuterated lipids (Buldt et al., 1979; Zaccai et al., 1979)
where the D-spacing was 54.1Å, are biologically less relevant.
One likely source of error in the
gravimetric method is the assumption that all the water resides neatly between
the bilayers (Wiener et al., 1989; Klose et al., 1988). This is
quite unlikely for multilamellar vesicles that must have
extra water in small volumes in the center of each MLV as well as in
regions between different MLVs. Only in well-oriented planar
arrays could one hope that this assumption is valid.
Also, the areas A from gravimetric studies have been consistently
larger than those obtained by other methods; this discrepancy is also
explained by the assumption about water residence being incorrect. In the case of gel
phase DPPC, we have shown previously for both oriented (Tristram-Nagle et al., 1993)
and powder, multilamellar vesicular samples (Sun et al., 1994),
that the gravimetric method gave erroneously large results for A.
Although our present results do not go to low enough hydration to
find the value of the dehydration threshold
,
above which the bilayer structure effectively does not change, must be
smaller than 54Å.
This conclusion is supported by the results of Torbet and Wilkins
(1976) for the gel phase of DPPC which showed that fairly small changes
in bilayer thickness resulted in rather large changes in the continuous
transform. This conclusion disagrees with
conclusions drawn from x-ray studies using the gravimetric method of
Luzzati which indicated that bilayer structure changed continuously
as the system is dehydrated from full hydration (Tardieu et al., 1973; Lis et al., 1982).
The latter conclusion had implied that results from studies on partially dehydrated
samples, such as the classic neutron diffraction studies on
specifically deuterated lipids (Buldt et al., 1979; Zaccai et al., 1979)
where the D-spacing was 54.1Å, are biologically less relevant.
One likely source of error in the
gravimetric method is the assumption that all the water resides neatly between
the bilayers (Wiener et al., 1989; Klose et al., 1988). This is
quite unlikely for multilamellar vesicles that must have
extra water in small volumes in the center of each MLV as well as in
regions between different MLVs. Only in well-oriented planar
arrays could one hope that this assumption is valid.
Also, the areas A from gravimetric studies have been consistently
larger than those obtained by other methods; this discrepancy is also
explained by the assumption about water residence being incorrect. In the case of gel
phase DPPC, we have shown previously for both oriented (Tristram-Nagle et al., 1993)
and powder, multilamellar vesicular samples (Sun et al., 1994),
that the gravimetric method gave erroneously large results for A.
Although our present results do not go to low enough hydration to
find the value of the dehydration threshold 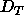 , they do require
that
, they do require
that 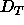 be smaller than 54Å and this suffices to validate the
biological relevance of the neutron diffraction results for
be smaller than 54Å and this suffices to validate the
biological relevance of the neutron diffraction results for 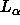 phase DPPC at
phase DPPC at 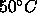 as well as
to provide support for x-ray studies that attempt to obtain membrane
structure for partially dehydrated samples.
as well as
to provide support for x-ray studies that attempt to obtain membrane
structure for partially dehydrated samples.
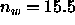 waters even when
waters even when 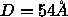 .
This is even more water than resides in the fully hydrated gel phase.
Also, the mean pure water spacing
.
This is even more water than resides in the fully hydrated gel phase.
Also, the mean pure water spacing 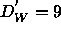 Å between headgroups is
still large enough to avoid much direct contact between headgroups
on adjacent bilayers because, as shown by Zhang et al. (1995b),
the mean fluctuation in adjacent bilayer
spacing is only about
Å between headgroups is
still large enough to avoid much direct contact between headgroups
on adjacent bilayers because, as shown by Zhang et al. (1995b),
the mean fluctuation in adjacent bilayer
spacing is only about 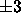 Å for the value of
Å for the value of 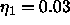 that is obtained for D = 54Å from Fig.
that is obtained for D = 54Å from Fig. 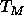 rises
at most
rises
at most 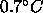 ; this is much less than the rise in
; this is much less than the rise in 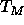 for
fully dehydrated samples which exceeds
for
fully dehydrated samples which exceeds 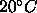 . Finally,
the work W done against the hydration force is given by the
product of the osmotic pressure of our most dehydrated
sample (
. Finally,
the work W done against the hydration force is given by the
product of the osmotic pressure of our most dehydrated
sample (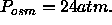 ), the area
), the area 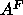 and the decay length
and the decay length
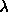 , which is given as 1.7Å for egg lecithin (McIntosh and Simon, 1986a);
this yields 0.03 kcal/mol, which is considerably less than the
enthalpy 8.7kcal/mol for the main phase transition which sets the
scale for major structural changes. Therefore, our experimental
result that bilayer structure does not change measurably upon dehydrating
to D=54Å is theoretically plausible and consistent with our
determination of structure reported in Table II.
, which is given as 1.7Å for egg lecithin (McIntosh and Simon, 1986a);
this yields 0.03 kcal/mol, which is considerably less than the
enthalpy 8.7kcal/mol for the main phase transition which sets the
scale for major structural changes. Therefore, our experimental
result that bilayer structure does not change measurably upon dehydrating
to D=54Å is theoretically plausible and consistent with our
determination of structure reported in Table II.
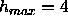 . Earlier use of this procedure has also indicated
that the thickness of bilayers does not change upon dehydrating with
PVP for either the gel phase of DPPC or the
. Earlier use of this procedure has also indicated
that the thickness of bilayers does not change upon dehydrating with
PVP for either the gel phase of DPPC or the 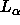 phase of
egg lecithin (McIntosh, 1986a). One of our concerns with this earlier conclusion
was that fluctuation corrections were not made
and that this would be expected to distort the form factors as shown
in Fig.
phase of
egg lecithin (McIntosh, 1986a). One of our concerns with this earlier conclusion
was that fluctuation corrections were not made
and that this would be expected to distort the form factors as shown
in Fig. 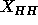 and this was
the major result required by the earlier work. Since only the
widths of the peaks and the methyl troughs are affected, our results
therefore support the methodology of the earlier work as well as the
conclusion that there is little change in bilayer structure upon mild dehydration.
and this was
the major result required by the earlier work. Since only the
widths of the peaks and the methyl troughs are affected, our results
therefore support the methodology of the earlier work as well as the
conclusion that there is little change in bilayer structure upon mild dehydration.
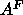 for
for 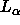 phase DPPC at 50
phase DPPC at 50 C, which is the most commonly
compared temperature. Although
C, which is the most commonly
compared temperature. Although 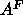 does not depend upon hydration down
to the
does not depend upon hydration down
to the 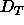 threshold, it is expected to depend fairly strongly on
temperature, especially near the main transition
threshold, it is expected to depend fairly strongly on
temperature, especially near the main transition 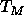 (Zhang et al., 1995a),
as well as exhibiting a gradual increase with increasing T above
50
(Zhang et al., 1995a),
as well as exhibiting a gradual increase with increasing T above
50 C, but we have not included these effects in this study.
Our primary method was adapted from one introduced by McIntosh and Simon (1986b)
that obtains
C, but we have not included these effects in this study.
Our primary method was adapted from one introduced by McIntosh and Simon (1986b)
that obtains 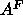 for the
for the 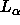 phase from Eq.
phase from Eq. 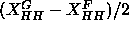 ,
which are obtained in this paper. The Fourier method
works quite well, yielding
,
which are obtained in this paper. The Fourier method
works quite well, yielding 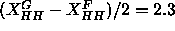 Å
and
Å
and 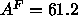 Å
Å , despite having only three samples with
, despite having only three samples with 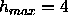 orders.
orders.
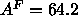 Å
Å .
.
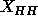 in the experimental electron density profiles in
Fig.
in the experimental electron density profiles in
Fig. 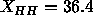 Å. One discrepancy that
arises is that use of this value of
Å. One discrepancy that
arises is that use of this value of 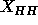 in Eq.
in Eq. 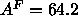 Å
Å which is larger than
which is larger than
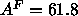 Å
Å obtained from the simulation. However, the same
spatial resolution and methodology should be used for both the gel and the
fluid phases in calculating the difference in
obtained from the simulation. However, the same
spatial resolution and methodology should be used for both the gel and the
fluid phases in calculating the difference in 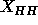 , so that we
should use the value
, so that we
should use the value 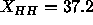 Å obtained from a 1G fit to
the simulated electron density profile (see Fig.
Å obtained from a 1G fit to
the simulated electron density profile (see Fig. 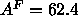 Å
Å from Eq.
from Eq. 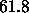 Å
Å and supports our methodology for obtaining
and supports our methodology for obtaining 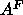 .
Another minor inconsistency arises from
applying Eq.
.
Another minor inconsistency arises from
applying Eq. 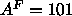 Å
Å assuming
that
assuming
that 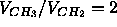 and that
and that 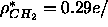 Å
Å ;
the latter value appears consistent with the simulated curve in
Fig.
;
the latter value appears consistent with the simulated curve in
Fig. 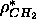 closer to
closer to 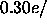 Å
Å . Using this latter value of
. Using this latter value of
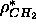 changes the size of the methyl trough so
that
changes the size of the methyl trough so
that 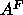 then yields 62Å
then yields 62Å using Eq.
using Eq. 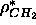 that emerge from the fit seem to be corrupted
by mixing with other parameters so that Eq.
that emerge from the fit seem to be corrupted
by mixing with other parameters so that Eq. 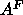 . Another discrepancy is that
our hybrid model headgroup peaks are much higher
than the simulated headgroup peaks in Fig.
. Another discrepancy is that
our hybrid model headgroup peaks are much higher
than the simulated headgroup peaks in Fig. 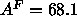 Å
Å and consequently have a smaller
and consequently have a smaller 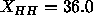 Å when fitted to
a 1G model.
Å when fitted to
a 1G model.
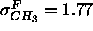 Å), not much wider than the
1G methyl trough for the gel phase (
Å), not much wider than the
1G methyl trough for the gel phase (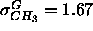 Å)
and narrower than the Gaussian fit to the simulation methyl trough
(
Å)
and narrower than the Gaussian fit to the simulation methyl trough
(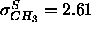 Å). The 1G headgroups have half-widths
(
Å). The 1G headgroups have half-widths
(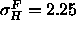 Å) which are narrower than the gel phase
results (
Å) which are narrower than the gel phase
results (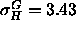 Å) and the fluid phase simulations
(
Å) and the fluid phase simulations
(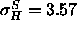 Å). It is possible that the narrowness of our
model electron density profiles is related to intrinsic errors
in analytically continuing the F(q) curve to high q. Although
the lack of data at higher angles always broadens
features in Fourier reconstructions of the electron density profile,
this is not necessarily the case for the model method,
as we have confirmed by taking a known model electron density profile,
Fourier analyzing it, adding noise to the Fouriers, fitting models
to the Fouriers, and then comparing to the original model
electron density.
Finally, when we did a fit with all three constraints, but with
Å). It is possible that the narrowness of our
model electron density profiles is related to intrinsic errors
in analytically continuing the F(q) curve to high q. Although
the lack of data at higher angles always broadens
features in Fourier reconstructions of the electron density profile,
this is not necessarily the case for the model method,
as we have confirmed by taking a known model electron density profile,
Fourier analyzing it, adding noise to the Fouriers, fitting models
to the Fouriers, and then comparing to the original model
electron density.
Finally, when we did a fit with all three constraints, but with
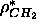 fixed to 0.304e/Å
fixed to 0.304e/Å , the methyl trough half-width
increased substantially to
, the methyl trough half-width
increased substantially to 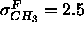 Å. In contrast,
Å. In contrast,
 only increased by 0.1Å, so widths of features in the
hybrid model may be less certain than the head-head spacing,
which is the crucial quantity for obtaining the area
only increased by 0.1Å, so widths of features in the
hybrid model may be less certain than the head-head spacing,
which is the crucial quantity for obtaining the area 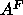 .
.
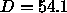 Å, in two new ways to
obtain additional estimates,
Å, in two new ways to
obtain additional estimates, 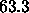 Å
Å and
and 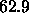 Å
Å , for
, for 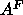 .
For our final estimate of
.
For our final estimate of 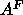 , we averaged these with
two x-ray results,
, we averaged these with
two x-ray results, 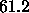 Å
Å from Fourier analysis and
from Fourier analysis and 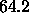 Å
Å from hybrid modeling to obtain our final diffraction result,
from hybrid modeling to obtain our final diffraction result,
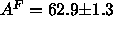 Å
Å in the
in the 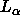 phase of DPPC at 50
phase of DPPC at 50 C.
C.
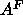 uses the
uses the 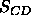 NMR order parameters.
Although the NMR method has been
employed in several different ways giving considerably different values
of
NMR order parameters.
Although the NMR method has been
employed in several different ways giving considerably different values
of 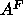 , our recent analysis gave
, our recent analysis gave 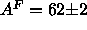 Å
Å for DPPC under the same conditions as in this paper (Nagle, 1993), in
good agreement with the present diffraction result. Even the sign of the
small difference can be understood because the NMR result assumed no
backtracking of chains, which, if present, would increase the NMR estimate
of
for DPPC under the same conditions as in this paper (Nagle, 1993), in
good agreement with the present diffraction result. Even the sign of the
small difference can be understood because the NMR result assumed no
backtracking of chains, which, if present, would increase the NMR estimate
of 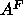 . As more quantitative information about backtracking becomes
available from simulations, quantitative changes in the NMR estimate
can be made.
. As more quantitative information about backtracking becomes
available from simulations, quantitative changes in the NMR estimate
can be made.
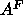 is smaller than the value
is smaller than the value 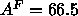 Å
Å determined for unilamellar vesicles by Lewis and Engelman (1983) using weak
continuous scattering. It is
considerably smaller than the
determined for unilamellar vesicles by Lewis and Engelman (1983) using weak
continuous scattering. It is
considerably smaller than the 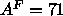 Å
Å obtained by
the gravimetric method (Lis et al., 1982) or the
obtained by
the gravimetric method (Lis et al., 1982) or the 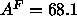 Å
Å obtained
by modifying that method (Rand and Parsegian, 1989) to try to account
for inconsistency with lateral compressibility data. This latter value of
obtained
by modifying that method (Rand and Parsegian, 1989) to try to account
for inconsistency with lateral compressibility data. This latter value of 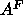 was assumed in the simulations of Feller et al. (1995). A recent simulation
(Essmann et al., 1995) used a fixed value
was assumed in the simulations of Feller et al. (1995). A recent simulation
(Essmann et al., 1995) used a fixed value 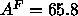 Å
Å for
nearly fully hydrated DPPC with
for
nearly fully hydrated DPPC with 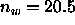 . Other recent simulations
employ constant pressure ensembles rather than constant area
ensembles and this allows for the simulation to determine the best
. Other recent simulations
employ constant pressure ensembles rather than constant area
ensembles and this allows for the simulation to determine the best 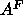 .
Chiu et al. (1995) obtain the rather smaller
.
Chiu et al. (1995) obtain the rather smaller
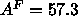 Å
Å at 52
at 52 C, but this was for DMPC. The recent simulations
for DPPC by Tu et al. (1995) yield
C, but this was for DMPC. The recent simulations
for DPPC by Tu et al. (1995) yield 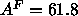 Å
Å , in excellent
agreement with our values for
, in excellent
agreement with our values for 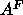 .
.
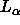 phase lipid bilayers are difficult to study experimentally,
due to their partially ordered/disordered nature which gives rise
to non-trivial fluctuations. We believe the present study has made
substantial progress on this point. We anticipate that combined experimental
and simulation studies will resolve remaining issues and provide a
methodological foundation for quantitatively comparing bilayers composed of
different lipids.
phase lipid bilayers are difficult to study experimentally,
due to their partially ordered/disordered nature which gives rise
to non-trivial fluctuations. We believe the present study has made
substantial progress on this point. We anticipate that combined experimental
and simulation studies will resolve remaining issues and provide a
methodological foundation for quantitatively comparing bilayers composed of
different lipids.