


Next: Fourier reconstruction of electon
Up: RESULTS
Previous: Basic Data: Form Factors
The first major issue to test with the data in Table I is whether
(i) partial dehydration changes the structure of the bilayer, such as the thickness,
or whether (ii) partial dehydration consists simply of taking water out of the
space between bilayers leaving the bilayers essentially unchanged.
It is unlikely that bilayer structure will remain unchanged for strong
dehydration that removes nearly all the water, so it is important to
emphasize that the word partial in the statement of the hypothesis in (ii)
means that there is a threshold spacing 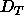 smaller than
the fully hydrated spacing
smaller than
the fully hydrated spacing 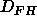 such that for D spacing between
such that for D spacing between
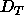 and
and 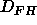 there is no effective change in bilayer structure.
We will refer to hypothesis (ii) as the threshold hypothesis.
Although it is likely that there will be an effect on the bilayer
structure caused by any change in interlamellar forces that must
accompany any level of dehydration, the effect would be expected
to be negligible for mild dehydration if the interlamellar
interactions are weak compared to the intralamellar interactions when the
water spacing is large enough (Nagle, 1980).
there is no effective change in bilayer structure.
We will refer to hypothesis (ii) as the threshold hypothesis.
Although it is likely that there will be an effect on the bilayer
structure caused by any change in interlamellar forces that must
accompany any level of dehydration, the effect would be expected
to be negligible for mild dehydration if the interlamellar
interactions are weak compared to the intralamellar interactions when the
water spacing is large enough (Nagle, 1980).
The standard way to test the dehydration hypothesis is to observe whether
the form factors for all the samples fall on a single continuous transform
F(q) (Torbet and Wilkins, 1976; McIntosh and Simon, 1986a).
In this subsection this is accomplished first by obtaining a trial F(q) using
the sampling theorem (Worthington et al., 1973) and four measured orders of
diffraction from one of the more dehydrated samples. A scale factor
is then chosen for each remaining sample to minimize the weighted
differences of the discrete form factors with the trial F(q).
The result of this procedure, shown in Fig. 4, indicates that the
fluctuation corrected form factors belong to a single continuous transform,
thereby supporting the threshold hypothesis and negligible change in
bilayer structure over the range of dehydration of our data.
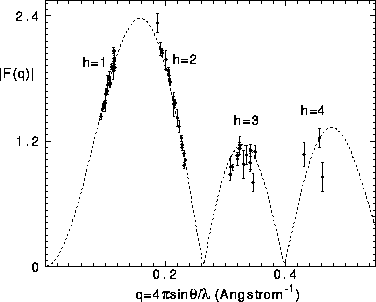
Figure 4: The dashed curve shows the continuous transform obtained
from the four orders of the D=55.06Å sample. The solid circles show
the corrected form factors for all 21 samples, each set of form factors for
each sample scaled simultaneously for all orders to give the best fit to the
dashed curve. F(0) is set to zero from volume measurements.
Figure 4 is drawn with F(0) = 0. This value follows from
the general relation for the minus-fluid form factor (Nagle and Wiener, 1989),

Using the number of electrons 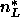 = 406 in a DPPC molecule,
the measured volume of DPPC molecules
= 406 in a DPPC molecule,
the measured volume of DPPC molecules 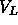 = 1232Å
= 1232Å at 50
at 50 C (Nagle and Wiener, 1988) , and the density of
electrons in water
C (Nagle and Wiener, 1988) , and the density of
electrons in water 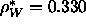 Å
Å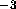 at 50
at 50 C gives a nearly zero numerator on the right hand
side of Eq. 4 so that
for any reasonable estimate of A one has F(0) about -0.02e/Å
C gives a nearly zero numerator on the right hand
side of Eq. 4 so that
for any reasonable estimate of A one has F(0) about -0.02e/Å .
The value of F(0) is 1.0e/Å
.
The value of F(0) is 1.0e/Å for the gel phase (Wiener et al., 1989)
and the absolute values of
for the gel phase (Wiener et al., 1989)
and the absolute values of 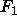 (to be obtained later) exceed 2e/Å
(to be obtained later) exceed 2e/Å .
Compared with these, F(0) for the fluid phase is negligible and will be
taken to be zero in this paper.
.
Compared with these, F(0) for the fluid phase is negligible and will be
taken to be zero in this paper.
It is important to examine why our corrections to the form factors
are essential. Figure 5 shows a continuous F(q) curve obtained
from uncorrected form factors in the same way as the F(q) curve
in Fig. 4 was obtained from the corrected form factors.
In Fig. 5 all the first
order form factors have been placed on the F(q) curve.
Then, it is seen that the second order form factors also
fall on the F(q) curve for small D, but that for D greater
than 61Å (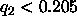 Å
Å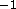 ) the second order
form factors systematically
fall below the F(q) curve. If one had no reason to correct these
form factors, one would have to draw the conclusion that
the bilayer structure changes as full hydration is
approached. However, this conclusion is not warranted because
these are the form factors
that require the largest corrections because
) the second order
form factors systematically
fall below the F(q) curve. If one had no reason to correct these
form factors, one would have to draw the conclusion that
the bilayer structure changes as full hydration is
approached. However, this conclusion is not warranted because
these are the form factors
that require the largest corrections because 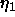 is
greatest for these samples. As is shown in Fig. 4 the corrections
bring these form factors back onto the F(q) curve. A similar,
but less dramatic, trend occurs for the h=3 form factors with
the largest D spacings. In Fig. 5 estimated ranges
(as indicated in Table I by c entries) are shown for peaks that
we attempted to observe but could not because they were too weak;
the largest value for these ranges indicates our estimate
of the smallest peak that we could have seen with our apparatus.
The unobservability of the
h=4 peaks is not surprising since most of them have q values that fall
near a zero in the F(q) transform. However, some of the unobserved
h=3 peaks would, without our correction theory, not follow the F(q)
curve and would therefore also lead to the erroneous conclusion that the bilayer
structure changes as full hydration is approached. Because the correction
for these unobserved peaks is even larger than
is
greatest for these samples. As is shown in Fig. 4 the corrections
bring these form factors back onto the F(q) curve. A similar,
but less dramatic, trend occurs for the h=3 form factors with
the largest D spacings. In Fig. 5 estimated ranges
(as indicated in Table I by c entries) are shown for peaks that
we attempted to observe but could not because they were too weak;
the largest value for these ranges indicates our estimate
of the smallest peak that we could have seen with our apparatus.
The unobservability of the
h=4 peaks is not surprising since most of them have q values that fall
near a zero in the F(q) transform. However, some of the unobserved
h=3 peaks would, without our correction theory, not follow the F(q)
curve and would therefore also lead to the erroneous conclusion that the bilayer
structure changes as full hydration is approached. Because the correction
for these unobserved peaks is even larger than 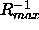 shown in
Table I, the corrected ranges are larger than shown in Fig. 5 and
overlap the continuous transform in Fig. 4.
shown in
Table I, the corrected ranges are larger than shown in Fig. 5 and
overlap the continuous transform in Fig. 4.
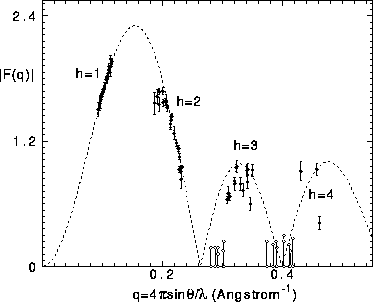
Figure 5: The dashed curve shows the continuous transform obtained
from the uncorrected four orders of the D=55.06Å sample.
The solid circles show the form factors for all 21 samples with
each F(1) placed on the F(q) curve. Open circles indicate
peaks not seen whose uncorrected form factors are estimated to
be bounded by the pair of circles joined by a vertical line.



Next: Fourier reconstruction of electon
Up: RESULTS
Previous: Basic Data: Form Factors
This document was converted to HTML by Nikolai Gouliaev on Fri Oct 4 15:28:39 EDT 1996
Your comments are welcome at gouliaev@andrew.cmu.edu
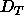 smaller than
the fully hydrated spacing
smaller than
the fully hydrated spacing 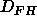 such that for D spacing between
such that for D spacing between
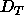 and
and 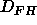 there is no effective change in bilayer structure.
We will refer to hypothesis (ii) as the threshold hypothesis.
Although it is likely that there will be an effect on the bilayer
structure caused by any change in interlamellar forces that must
accompany any level of dehydration, the effect would be expected
to be negligible for mild dehydration if the interlamellar
interactions are weak compared to the intralamellar interactions when the
water spacing is large enough (Nagle, 1980).
there is no effective change in bilayer structure.
We will refer to hypothesis (ii) as the threshold hypothesis.
Although it is likely that there will be an effect on the bilayer
structure caused by any change in interlamellar forces that must
accompany any level of dehydration, the effect would be expected
to be negligible for mild dehydration if the interlamellar
interactions are weak compared to the intralamellar interactions when the
water spacing is large enough (Nagle, 1980).


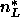 = 406 in a DPPC molecule,
the measured volume of DPPC molecules
= 406 in a DPPC molecule,
the measured volume of DPPC molecules 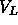 = 1232Å
= 1232Å at 50
at 50 C (Nagle and Wiener, 1988) , and the density of
electrons in water
C (Nagle and Wiener, 1988) , and the density of
electrons in water 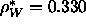 Å
Å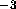 at 50
at 50 C gives a nearly zero numerator on the right hand
side of Eq.
C gives a nearly zero numerator on the right hand
side of Eq.  .
The value of F(0) is 1.0e/Å
.
The value of F(0) is 1.0e/Å for the gel phase (Wiener et al., 1989)
and the absolute values of
for the gel phase (Wiener et al., 1989)
and the absolute values of 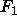 (to be obtained later) exceed 2e/Å
(to be obtained later) exceed 2e/Å .
Compared with these, F(0) for the fluid phase is negligible and will be
taken to be zero in this paper.
.
Compared with these, F(0) for the fluid phase is negligible and will be
taken to be zero in this paper.
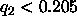 Å
Å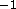 ) the second order
form factors systematically
fall below the F(q) curve. If one had no reason to correct these
form factors, one would have to draw the conclusion that
the bilayer structure changes as full hydration is
approached. However, this conclusion is not warranted because
these are the form factors
that require the largest corrections because
) the second order
form factors systematically
fall below the F(q) curve. If one had no reason to correct these
form factors, one would have to draw the conclusion that
the bilayer structure changes as full hydration is
approached. However, this conclusion is not warranted because
these are the form factors
that require the largest corrections because 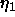 is
greatest for these samples. As is shown in Fig.
is
greatest for these samples. As is shown in Fig. 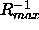 shown in
Table I, the corrected ranges are larger than shown in Fig. 5 and
overlap the continuous transform in Fig. 4.
shown in
Table I, the corrected ranges are larger than shown in Fig. 5 and
overlap the continuous transform in Fig. 4.
