


Next: Hybrid Models
Up: RESULTS
Previous: Fourier reconstruction of electon
One of our main goals has been to obtain the area A per lipid molecule
at the water/bilayer interface. Since this involves information
about the structure in the direction along the surface of the
bilayer, whereas low angle scattering involves information along
the direction of the bilayer normal, other information must be
used. We will adapt a method introduced by McIntosh and Simon
(1986b) and applied by them to DLPE. This method makes use
of the well-determined gel phase quantities and of measured differences
with the 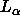 phase. The quantities involved are
area A, lipid volume
phase. The quantities involved are
area A, lipid volume 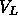 , hydrocarbon chain thickness
, hydrocarbon chain thickness 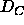 which
is half the thickness of the hydrocarbon region in a bilayer, and head-head
spacing
which
is half the thickness of the hydrocarbon region in a bilayer, and head-head
spacing 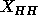 ; superscript G will designate gel phase and
superscript F will designate fluid (
; superscript G will designate gel phase and
superscript F will designate fluid (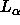 ) phase
quantities. The method begins with the statement that the change
in volume takes place only in the hydrocarbon region, so
) phase
quantities. The method begins with the statement that the change
in volume takes place only in the hydrocarbon region, so

The justification for assuming that there is little change in
volume of the headgroup region is that water can freely enter
this region and fill any volume that is voided by the headgroups
in going from the gel to the fluid phase (see Wiener et al. (1988)
or Nagle and Wilkinson (1978) for more discussion of this assumption).
We next write

which assumes that the major determinant of changes in 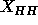 is changes in the hydrocarbon region. Even though the headgroups might
be expected to adopt a different mixture of conformations in
the two phases, the lever arm for distance changes due to
headgroup changes is short, essentially from the carbonyls to the
phosphate since the choline is not electron dense,
so that Eq. 6 should be
a reasonable first approximation. It may be noted, however,
that the assumptions behind both Eq. 5 and Eq. 6
should be subject to testing and possible modification by molecular
dynamics simulations. Solving Eqs. 5 and 6
yields
is changes in the hydrocarbon region. Even though the headgroups might
be expected to adopt a different mixture of conformations in
the two phases, the lever arm for distance changes due to
headgroup changes is short, essentially from the carbonyls to the
phosphate since the choline is not electron dense,
so that Eq. 6 should be
a reasonable first approximation. It may be noted, however,
that the assumptions behind both Eq. 5 and Eq. 6
should be subject to testing and possible modification by molecular
dynamics simulations. Solving Eqs. 5 and 6
yields
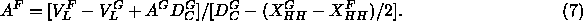
To apply Eq. 7 we use volume measurements summarized by Nagle and Wiener
(1988) which gave 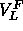 =1232Å
=1232Å at 50
at 50 C and
C and 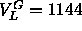 Å
Å at 20
at 20 C. Our best wide angle x-ray
determination of the gel phase (Sun et al., 1994) gives
C. Our best wide angle x-ray
determination of the gel phase (Sun et al., 1994) gives 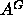 =47.9
=47.9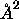 and
and 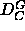 =17.23
=17.23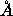 (corrected from
(corrected from 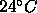 to
to 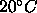 ).
Using the values
).
Using the values 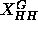 =44.2Å and
=44.2Å and 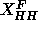 =39.6Å
obtained from Fig. 6 and the preceding subsection and using Eq. 7
then gives
=39.6Å
obtained from Fig. 6 and the preceding subsection and using Eq. 7
then gives 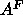 = 61.2Å
= 61.2Å .
.



Next: Hybrid Models
Up: RESULTS
Previous: Fourier reconstruction of electon
This document was converted to HTML by Nikolai Gouliaev on Fri Oct 4 15:28:39 EDT 1996
Your comments are welcome at gouliaev@andrew.cmu.edu
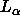 phase. The quantities involved are
area A, lipid volume
phase. The quantities involved are
area A, lipid volume 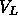 , hydrocarbon chain thickness
, hydrocarbon chain thickness 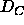 which
is half the thickness of the hydrocarbon region in a bilayer, and head-head
spacing
which
is half the thickness of the hydrocarbon region in a bilayer, and head-head
spacing 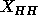 ; superscript G will designate gel phase and
superscript F will designate fluid (
; superscript G will designate gel phase and
superscript F will designate fluid (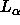 ) phase
quantities. The method begins with the statement that the change
in volume takes place only in the hydrocarbon region, so
) phase
quantities. The method begins with the statement that the change
in volume takes place only in the hydrocarbon region, so


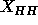 is changes in the hydrocarbon region. Even though the headgroups might
be expected to adopt a different mixture of conformations in
the two phases, the lever arm for distance changes due to
headgroup changes is short, essentially from the carbonyls to the
phosphate since the choline is not electron dense,
so that Eq.
is changes in the hydrocarbon region. Even though the headgroups might
be expected to adopt a different mixture of conformations in
the two phases, the lever arm for distance changes due to
headgroup changes is short, essentially from the carbonyls to the
phosphate since the choline is not electron dense,
so that Eq. 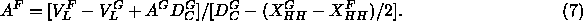
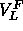 =1232Å
=1232Å at 50
at 50 C and
C and 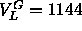 Å
Å at 20
at 20 C. Our best wide angle x-ray
determination of the gel phase (Sun et al., 1994) gives
C. Our best wide angle x-ray
determination of the gel phase (Sun et al., 1994) gives 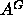 =47.9
=47.9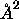 and
and 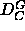 =17.23
=17.23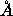 (corrected from
(corrected from 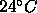 to
to 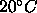 ).
Using the values
).
Using the values 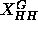 =44.2Å and
=44.2Å and 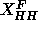 =39.6Å
obtained from Fig.
=39.6Å
obtained from Fig. 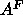 = 61.2Å
= 61.2Å .
.