


Next: from Neutron Diffraction Studies
Up: RESULTS
Previous: Method for Determining A
Fourier reconstruction of electron density profiles has some disadvantages;
(i) it is intrinsically on a relative scale rather than an absolute scale,
(ii) it can only use form factors from one sample at a time, and
(iii) it has obviously unreal Fourier wiggles.
An alternative is to specify a reasonable functional form
for the electron density that involves several parameters that are then fit
to provide the best agreement with the measured intensities. (Notice that
the phases of the form factors are output, not input.)
The particular electron density model that will be employed in
this subsection is called the 1G hybrid model (Nagle and Wiener, 1989).
This model has one Gaussian representing each headgroup with three parameters
(position, width and height), a Gaussian methyl trough with
two parameters (width and depth with position fixed at zero),
a known constant water electron density and a constant methylene electron
density 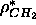 . If one of the electron density amplitude
parameters can be predetermined, then hybrid model electron densities can be put
on an absolute scale. Furthermore, all the form factors for all
the data from different samples at different D spacings can be
used on an equal footing to determine the best values of the
parameters in the model. We have measured 59 form factors,
many more than the number 21 of scaling factors
plus the number of unknown parameters (6 for the 1G hybrid
model described above and 9 if two Gaussians represent each
headgroup as in a 2G hybrid model). If there were no experimental error in the form factors,
these data would allow determination of quite realistic electron density
models with many parameters, as we have shown by simulated examples.
Indeed, in principle, the high q part of F(q) could be obtained by
analytic continuation of the low q portion. In practice,
there is experimental error that leads to uncertainty in extrapolation from
low q to high q, so one can not expect to separate
structural features, such as two Gaussians in the headgroup region, that are
much closer together than D/
. If one of the electron density amplitude
parameters can be predetermined, then hybrid model electron densities can be put
on an absolute scale. Furthermore, all the form factors for all
the data from different samples at different D spacings can be
used on an equal footing to determine the best values of the
parameters in the model. We have measured 59 form factors,
many more than the number 21 of scaling factors
plus the number of unknown parameters (6 for the 1G hybrid
model described above and 9 if two Gaussians represent each
headgroup as in a 2G hybrid model). If there were no experimental error in the form factors,
these data would allow determination of quite realistic electron density
models with many parameters, as we have shown by simulated examples.
Indeed, in principle, the high q part of F(q) could be obtained by
analytic continuation of the low q portion. In practice,
there is experimental error that leads to uncertainty in extrapolation from
low q to high q, so one can not expect to separate
structural features, such as two Gaussians in the headgroup region, that are
much closer together than D/ . Nevertheless, it would appear that
the model approach might still improve upon Fourier reconstructions and
should certainly be employed as a supplement.
. Nevertheless, it would appear that
the model approach might still improve upon Fourier reconstructions and
should certainly be employed as a supplement.
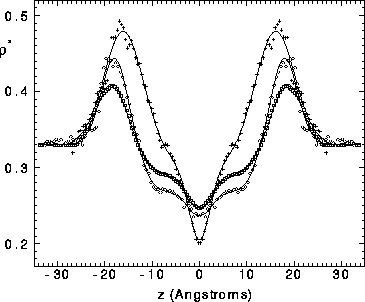
Figure 7: Symbols are symmetrized electron densities from three
molecular dynamics simulations: open squares, Tu et al. (1995);
open circles, Feller et al. (1995); +, Chiu et al. (1995).
The solid lines show the best fitted hybrid electron density models
with one Gaussian in the headgroup region.
The preceding argument in favor of electron density models
hinges substantially upon how well the true electron density
is represented by the particular model functional form chosen. We have tested the
hybrid models by fitting them to two molecular dynamics simulations of
electron density for DPPC (Tu et al., 1995; Feller et al., 1995)
and one for DMPC (Chiu et al., 1995), as shown in Fig. 7.
The 1G hybrid model provides quite a good representation of all three
sets of simulation data. Due to asymmetry,
employing two Gaussians (2G model) in the headgroup region does improve
the fit (not shown) to the results of Tu et al. (1995) and the headgroup
peaks of the results of Feller et al. (1995) are decidedly not symmetric,
though with the opposite asymmetry as the headgroup peaks of Tu et al. (1995).
The hybrid models were designed with the assumption (i) that each
methylene volume 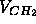 is nearly constant whether it is near the center of
the bilayer or nearer the headgroups (Nagle and Wiener, 1989).
It has also been assumed (Nagle and Wiener, 1988), from liquid alkane studies,
(ii) that the terminal methyls on the hydrocarbon chains have about twice the volumes
of the methylenes,
is nearly constant whether it is near the center of
the bilayer or nearer the headgroups (Nagle and Wiener, 1989).
It has also been assumed (Nagle and Wiener, 1988), from liquid alkane studies,
(ii) that the terminal methyls on the hydrocarbon chains have about twice the volumes
of the methylenes, 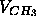 =2
=2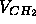 . If assumptions (i) and (ii) are true,
then the effective hydrocarbon number density, defined as
. If assumptions (i) and (ii) are true,
then the effective hydrocarbon number density, defined as 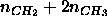 ,
should be constant as a function of z along the bilayer normal in
the central hydrocarbon region that is seldom penetrated by other groups.
The results of the simulations shown in Figure 8 basically support
these assumptions, especially the simulations
of Tu et al. (1995) which give quite constant effective hydrocarbon number
in the hydrocarbon region.
,
should be constant as a function of z along the bilayer normal in
the central hydrocarbon region that is seldom penetrated by other groups.
The results of the simulations shown in Figure 8 basically support
these assumptions, especially the simulations
of Tu et al. (1995) which give quite constant effective hydrocarbon number
in the hydrocarbon region.
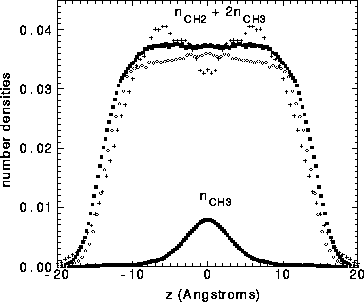
Figure: Effective hydrocarbon number densities
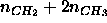 in units of Å
in units of Å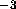 .
Solid squares from Tu et al. (1995); open circles
from Feller et al. (1995); + from Chiu et al. (1995).
Methyl number density is shown only for results
from Tu et al.
.
Solid squares from Tu et al. (1995); open circles
from Feller et al. (1995); + from Chiu et al. (1995).
Methyl number density is shown only for results
from Tu et al.
In addition to having to obey Eq. 4, which we will call the
F(0) constraint, there is a
second general relation for the hybrid models (Nagle and Wiener, 1989)
that relates A to the size, 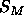 , of the methyl trough in the electron
density profile,
, of the methyl trough in the electron
density profile,

where 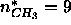 is the number of electrons in methyl groups.
In principle, this would be another way to determine A in addition
to Eq. 7. Unfortunately, our experience with fitting both
real and simulated data indicates that the errors in the values of
is the number of electrons in methyl groups.
In principle, this would be another way to determine A in addition
to Eq. 7. Unfortunately, our experience with fitting both
real and simulated data indicates that the errors in the values of 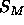 determined from unconstrained fits are too large for this method to
provide precise results for A. Instead, Eq. 8 has been
used to constrain the size
determined from unconstrained fits are too large for this method to
provide precise results for A. Instead, Eq. 8 has been
used to constrain the size 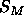 of the methyl trough using a value
of A=62Å
of the methyl trough using a value
of A=62Å ; this will be called the methyl
trough constraint. A third constraint, which will be called
the methylene constraint, was used extensively in modeling the gel
phase (Wiener et al., 1989). This constrains
the value of the methylene electron density
; this will be called the methyl
trough constraint. A third constraint, which will be called
the methylene constraint, was used extensively in modeling the gel
phase (Wiener et al., 1989). This constrains
the value of the methylene electron density 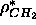 .
From volume measurements (Nagle and Wilkinson, 1978; Nagle
and Wiener, 1988)
.
From volume measurements (Nagle and Wilkinson, 1978; Nagle
and Wiener, 1988) 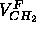 has been estimated to be 27.6Å
has been estimated to be 27.6Å ,
which yields
,
which yields 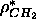 =0.290 electrons/Å
=0.290 electrons/Å .
.
Our results are shown in Fig. 9 for 1G electron density models.
We also attempted to fit 2G models, but there were many local minima found in the
fitting that corresponded to different proportions of the two head group
Gaussians and their locations; this confirms that the data
did not extend to high enough direct spatial resolution (not to be
confused with our high instrumental resolution in reciprocal
space) to distinguish fine features
of the headgroup region. Because it is desirable to compare to gel
phase electron densities at the same spatial resolution, the 1G
gel phase result with 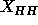 =42.4Å (Wiener et al., 1989)
is shown in Fig. 9.
=42.4Å (Wiener et al., 1989)
is shown in Fig. 9.
When none of the three constraints described above
are used, the hybrid model can not be put
on an absolute scale. This totally unconstrained fit can
be easily normalized by using the methylene constraint
and this is shown in Fig. 9 by the dotted curve. However,
the size of the methyl trough is so large that Eq. 8
gives the absurd value, 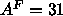 Å
Å . Another way to
scale this unconstrained fit is to impose the methyl trough constraint
instead of the methylene constraint; using
. Another way to
scale this unconstrained fit is to impose the methyl trough constraint
instead of the methylene constraint; using 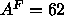 Å
Å reduces the sizes of the headgroup peaks and the methyl trough
by a factor of two and the ensuing curve (not shown) is in better
conformity with the other curves in Fig. 9 except that the
electron density in the methylene region increases to
reduces the sizes of the headgroup peaks and the methyl trough
by a factor of two and the ensuing curve (not shown) is in better
conformity with the other curves in Fig. 9 except that the
electron density in the methylene region increases to
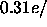 Å
Å . Also, with either of these constraints,
F(0) is strongly positive and the ratio of F(0) to F(1) is
of order
. Also, with either of these constraints,
F(0) is strongly positive and the ratio of F(0) to F(1) is
of order 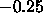 rather than close to zero as required by
volumetric data. Therefore, it is necessary to consider fits with
additional constraints. (It is worth noting, however, that
rather than close to zero as required by
volumetric data. Therefore, it is necessary to consider fits with
additional constraints. (It is worth noting, however, that
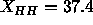 Å for the dashed line; by Eq. 7 this
gives
Å for the dashed line; by Eq. 7 this
gives 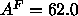 Å
Å .)
.)
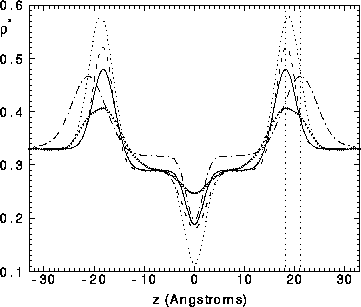
Figure 9: Several results for 1G models of the absolute
electron density 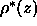 as a function of distance z along the
normal to the bilayer with the center of the bilayer at z=0.
Dot-dash line: gel phase.
Dotted line: methylene constraint only.
Dashed line: F(0) and methylene constraints.
Solid line: F(0), methylene and methyl trough constraints.
Small solid circles: simulation results from Tu et al. (1995).
The vertical dotted lines indicate the difference in half
as a function of distance z along the
normal to the bilayer with the center of the bilayer at z=0.
Dot-dash line: gel phase.
Dotted line: methylene constraint only.
Dashed line: F(0) and methylene constraints.
Solid line: F(0), methylene and methyl trough constraints.
Small solid circles: simulation results from Tu et al. (1995).
The vertical dotted lines indicate the difference in half 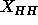 between the gel and the fluid phases.
between the gel and the fluid phases.
Since the 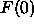 constraint appears to be experimentally
required, all our additional results use it. Unfortunately, since
F(0) is effectively zero, this
constraint does not allow the electron densities to be put
on an absolute scale. Therefore, our next model, shown
by the dashed line in Fig. 9, also adds the methylene constraint.
This model predicts, by Eq. 8, that
constraint appears to be experimentally
required, all our additional results use it. Unfortunately, since
F(0) is effectively zero, this
constraint does not allow the electron densities to be put
on an absolute scale. Therefore, our next model, shown
by the dashed line in Fig. 9, also adds the methylene constraint.
This model predicts, by Eq. 8, that 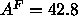 Å
Å ,
which is still smaller than
,
which is still smaller than 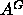 and the headgroup peaks are
rather large. We also tried using both the F(0) and the methyl trough
constraint but not the methylene constraint
(electron density profile not shown on Fig. 9) and this
resulted in a best value of
and the headgroup peaks are
rather large. We also tried using both the F(0) and the methyl trough
constraint but not the methylene constraint
(electron density profile not shown on Fig. 9) and this
resulted in a best value of 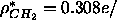 Å
Å which seems too high. We therefore finally fit the form factor
data with all three constraints. We used a trial value of
which seems too high. We therefore finally fit the form factor
data with all three constraints. We used a trial value of 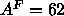 Å
Å in the methyl trough constraint, but all subsequent results, especially
the result for headgroup position
in the methyl trough constraint, but all subsequent results, especially
the result for headgroup position 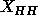 and the ensuing value of
and the ensuing value of
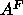 obtained from Eq. 7, are insensitive to 10% variations
in this trial value. We also favored fits that gave broader
electron density features and smaller F(q) values for
large q by adding zero values with noise levels comparable
to the data for eleven random q values greater than 0.6Å
obtained from Eq. 7, are insensitive to 10% variations
in this trial value. We also favored fits that gave broader
electron density features and smaller F(q) values for
large q by adding zero values with noise levels comparable
to the data for eleven random q values greater than 0.6Å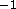 .
The resulting electron density profile is shown by the solid curve in
Fig. 9 and the continuous transform F(q) and the fit of the measured
form factors are shown in Fig. 10. The scaled values of F(1) that
appear in Table I correspond to Fig. 10. The electron density
profile shown by the solid curve in Fig. 9 gives
.
The resulting electron density profile is shown by the solid curve in
Fig. 9 and the continuous transform F(q) and the fit of the measured
form factors are shown in Fig. 10. The scaled values of F(1) that
appear in Table I correspond to Fig. 10. The electron density
profile shown by the solid curve in Fig. 9 gives 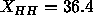 Å
which, by Eq. 7, gives
Å
which, by Eq. 7, gives 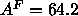 Å
Å . Although this
latter value of
. Although this
latter value of 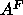 is different from the trial value of
is different from the trial value of 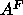 used in the methyl trough constraint, this makes very little difference in the
value of
used in the methyl trough constraint, this makes very little difference in the
value of 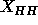 obtained from the fits.
obtained from the fits.
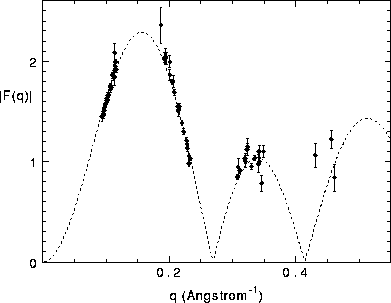
Figure: Best fit of 1G model to our data, with the methylene constraint,
methyl trough constraint, and the 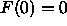 constraint. The dashed line is
the fit, and the solid circles are the form factor data for q less than
0.6Å
constraint. The dashed line is
the fit, and the solid circles are the form factor data for q less than
0.6Å .
.



Next: from Neutron Diffraction Studies
Up: RESULTS
Previous: Method for Determining A
This document was converted to HTML by Nikolai Gouliaev on Fri Oct 4 15:28:39 EDT 1996
Your comments are welcome at gouliaev@andrew.cmu.edu
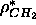 . If one of the electron density amplitude
parameters can be predetermined, then hybrid model electron densities can be put
on an absolute scale. Furthermore, all the form factors for all
the data from different samples at different D spacings can be
used on an equal footing to determine the best values of the
parameters in the model. We have measured 59 form factors,
many more than the number 21 of scaling factors
plus the number of unknown parameters (6 for the 1G hybrid
model described above and 9 if two Gaussians represent each
headgroup as in a 2G hybrid model). If there were no experimental error in the form factors,
these data would allow determination of quite realistic electron density
models with many parameters, as we have shown by simulated examples.
Indeed, in principle, the high q part of F(q) could be obtained by
analytic continuation of the low q portion. In practice,
there is experimental error that leads to uncertainty in extrapolation from
low q to high q, so one can not expect to separate
structural features, such as two Gaussians in the headgroup region, that are
much closer together than D/
. If one of the electron density amplitude
parameters can be predetermined, then hybrid model electron densities can be put
on an absolute scale. Furthermore, all the form factors for all
the data from different samples at different D spacings can be
used on an equal footing to determine the best values of the
parameters in the model. We have measured 59 form factors,
many more than the number 21 of scaling factors
plus the number of unknown parameters (6 for the 1G hybrid
model described above and 9 if two Gaussians represent each
headgroup as in a 2G hybrid model). If there were no experimental error in the form factors,
these data would allow determination of quite realistic electron density
models with many parameters, as we have shown by simulated examples.
Indeed, in principle, the high q part of F(q) could be obtained by
analytic continuation of the low q portion. In practice,
there is experimental error that leads to uncertainty in extrapolation from
low q to high q, so one can not expect to separate
structural features, such as two Gaussians in the headgroup region, that are
much closer together than D/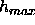 . Nevertheless, it would appear that
the model approach might still improve upon Fourier reconstructions and
should certainly be employed as a supplement.
. Nevertheless, it would appear that
the model approach might still improve upon Fourier reconstructions and
should certainly be employed as a supplement.

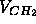 is nearly constant whether it is near the center of
the bilayer or nearer the headgroups (Nagle and Wiener, 1989).
It has also been assumed (Nagle and Wiener, 1988), from liquid alkane studies,
(ii) that the terminal methyls on the hydrocarbon chains have about twice the volumes
of the methylenes,
is nearly constant whether it is near the center of
the bilayer or nearer the headgroups (Nagle and Wiener, 1989).
It has also been assumed (Nagle and Wiener, 1988), from liquid alkane studies,
(ii) that the terminal methyls on the hydrocarbon chains have about twice the volumes
of the methylenes, 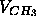 =2
=2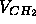 . If assumptions (i) and (ii) are true,
then the effective hydrocarbon number density, defined as
. If assumptions (i) and (ii) are true,
then the effective hydrocarbon number density, defined as 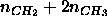 ,
should be constant as a function of z along the bilayer normal in
the central hydrocarbon region that is seldom penetrated by other groups.
The results of the simulations shown in Figure
,
should be constant as a function of z along the bilayer normal in
the central hydrocarbon region that is seldom penetrated by other groups.
The results of the simulations shown in Figure 
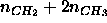 in units of Å
in units of Å .
Solid squares from Tu et al. (1995); open circles
from Feller et al. (1995); + from Chiu et al. (1995).
Methyl number density is shown only for results
from Tu et al.
.
Solid squares from Tu et al. (1995); open circles
from Feller et al. (1995); + from Chiu et al. (1995).
Methyl number density is shown only for results
from Tu et al.
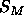 , of the methyl trough in the electron
density profile,
, of the methyl trough in the electron
density profile,

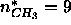 is the number of electrons in methyl groups.
In principle, this would be another way to determine A in addition
to Eq.
is the number of electrons in methyl groups.
In principle, this would be another way to determine A in addition
to Eq. 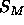 determined from unconstrained fits are too large for this method to
provide precise results for A. Instead, Eq.
determined from unconstrained fits are too large for this method to
provide precise results for A. Instead, Eq. 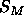 of the methyl trough using a value
of A=62Å
of the methyl trough using a value
of A=62Å ; this will be called the methyl
trough constraint. A third constraint, which will be called
the methylene constraint, was used extensively in modeling the gel
phase (Wiener et al., 1989). This constrains
the value of the methylene electron density
; this will be called the methyl
trough constraint. A third constraint, which will be called
the methylene constraint, was used extensively in modeling the gel
phase (Wiener et al., 1989). This constrains
the value of the methylene electron density 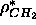 .
From volume measurements (Nagle and Wilkinson, 1978; Nagle
and Wiener, 1988)
.
From volume measurements (Nagle and Wilkinson, 1978; Nagle
and Wiener, 1988) 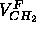 has been estimated to be 27.6Å
has been estimated to be 27.6Å ,
which yields
,
which yields 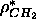 =0.290 electrons/Å
=0.290 electrons/Å .
.
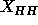 =42.4Å (Wiener et al., 1989)
is shown in Fig.
=42.4Å (Wiener et al., 1989)
is shown in Fig. 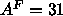 Å
Å . Another way to
scale this unconstrained fit is to impose the methyl trough constraint
instead of the methylene constraint; using
. Another way to
scale this unconstrained fit is to impose the methyl trough constraint
instead of the methylene constraint; using 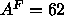 Å
Å reduces the sizes of the headgroup peaks and the methyl trough
by a factor of two and the ensuing curve (not shown) is in better
conformity with the other curves in Fig.
reduces the sizes of the headgroup peaks and the methyl trough
by a factor of two and the ensuing curve (not shown) is in better
conformity with the other curves in Fig. 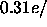 Å
Å . Also, with either of these constraints,
F(0) is strongly positive and the ratio of F(0) to F(1) is
of order
. Also, with either of these constraints,
F(0) is strongly positive and the ratio of F(0) to F(1) is
of order 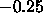 rather than close to zero as required by
volumetric data. Therefore, it is necessary to consider fits with
additional constraints. (It is worth noting, however, that
rather than close to zero as required by
volumetric data. Therefore, it is necessary to consider fits with
additional constraints. (It is worth noting, however, that
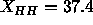 Å for the dashed line; by Eq.
Å for the dashed line; by Eq. 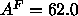 Å
Å .)
.)

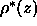 as a function of distance z along the
normal to the bilayer with the center of the bilayer at z=0.
Dot-dash line: gel phase.
Dotted line: methylene constraint only.
Dashed line: F(0) and methylene constraints.
Solid line: F(0), methylene and methyl trough constraints.
Small solid circles: simulation results from Tu et al. (1995).
The vertical dotted lines indicate the difference in half
as a function of distance z along the
normal to the bilayer with the center of the bilayer at z=0.
Dot-dash line: gel phase.
Dotted line: methylene constraint only.
Dashed line: F(0) and methylene constraints.
Solid line: F(0), methylene and methyl trough constraints.
Small solid circles: simulation results from Tu et al. (1995).
The vertical dotted lines indicate the difference in half 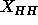 between the gel and the fluid phases.
between the gel and the fluid phases.
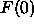 constraint appears to be experimentally
required, all our additional results use it. Unfortunately, since
F(0) is effectively zero, this
constraint does not allow the electron densities to be put
on an absolute scale. Therefore, our next model, shown
by the dashed line in Fig.
constraint appears to be experimentally
required, all our additional results use it. Unfortunately, since
F(0) is effectively zero, this
constraint does not allow the electron densities to be put
on an absolute scale. Therefore, our next model, shown
by the dashed line in Fig. 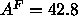 Å
Å ,
which is still smaller than
,
which is still smaller than 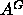 and the headgroup peaks are
rather large. We also tried using both the F(0) and the methyl trough
constraint but not the methylene constraint
(electron density profile not shown on Fig.
and the headgroup peaks are
rather large. We also tried using both the F(0) and the methyl trough
constraint but not the methylene constraint
(electron density profile not shown on Fig. 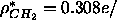 Å
Å which seems too high. We therefore finally fit the form factor
data with all three constraints. We used a trial value of
which seems too high. We therefore finally fit the form factor
data with all three constraints. We used a trial value of 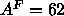 Å
Å in the methyl trough constraint, but all subsequent results, especially
the result for headgroup position
in the methyl trough constraint, but all subsequent results, especially
the result for headgroup position 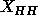 and the ensuing value of
and the ensuing value of
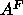 obtained from Eq.
obtained from Eq. 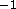 .
The resulting electron density profile is shown by the solid curve in
Fig.
.
The resulting electron density profile is shown by the solid curve in
Fig. 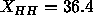 Å
which, by Eq.
Å
which, by Eq. 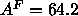 Å
Å . Although this
latter value of
. Although this
latter value of 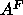 is different from the trial value of
is different from the trial value of 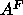 used in the methyl trough constraint, this makes very little difference in the
value of
used in the methyl trough constraint, this makes very little difference in the
value of  obtained from the fits.
obtained from the fits.

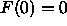 constraint. The dashed line is
the fit, and the solid circles are the form factor data for q less than
0.6Å
constraint. The dashed line is
the fit, and the solid circles are the form factor data for q less than
0.6Å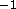 .
.